All the digital arithmetic circuits are designed by using logic gates where these gates are designed to perform binary addition and subtraction. In this article, we will see the basics of binary subtraction, which is one of the fundamental tasks to be performed by any microprocessor/microcontroller. These gates which perform subtraction are designed based on simple rules, which perform the logic operations. These rules follow a simple truth table, which is similar to traditional arithmetic rules. The results obtained by binary subtraction should match the results obtained by digital numbers obtained by binary to digital conversion.
What is Binary Subtraction?
Definition: Binary subtraction is a set of rules programmed to perform the subtraction of two numbers, which are represented in their binary form. These rules are based on the traditional methods of doing subtraction. Based on a set of rules, the logic gates are designed, and the logic gates perform subtraction. Before doing binary subtraction, one must be aware of the binary conversion or the binary equivalent of digital numbers. In the following figure, the equivalent is shown.
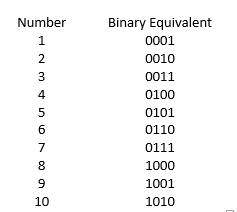
Binary Equivalent
Binary Subtraction Truth Table
The following figure represents the truth table for binary subtraction
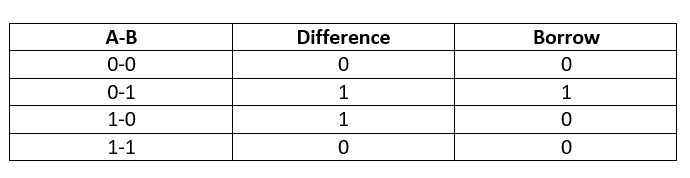
Binary Subtraction Truth Table
As shown in the figure, the difference between 0 and 0 is 0 with no borrow. In binary addition, the sum and carry are important, but in binary subtraction, the difference and borrow are considered. Let’s take the second case. Here 0 is subtracted from one, which results in a difference of 1. But 0 cannot be subtracted from one, for this, we need to take a borrow from the previous number.
The subtraction rules are adapted, from the subtraction rules of traditional numbers. For the third case, when 1 is subtracted from 0, the difference is one with no borrow required. Hence the borrow is also 0. And for the last case, when one is subtracted from one, the difference is zero with borrow also zero.
Binary Subtraction with Steps
Now let’s take an example. Consider the following table.

Binary Subtraction
Step 1.
Always the subtraction is started from the rightmost side. In the left-most part, we have two numbers, 0 and 0. From the truth table, we can see that the difference is 0 in this case. And no borrow is required. So the result is zero.
Step 2
Then, consider the next number. In this case, both the numbers are one and one. So, the difference is zero, with no borrow required. Hence, the result is 0 in this case.
Step 3.
For the next results, the numbers are the same as before. Which is zero and zero. Hence the result is zero in this case.
Step 4.
For the last numbers, we have one and zero. Since one is greater we don’t need any borrow in this case also. Hence, the result would be one with no borrow required.
Now let’s check our answers. The digital equivalent of the first number 1010 is 10, and the second number 0010 digital equivalent is two. Hence the subtraction should be equal to 10-2=8. The result is 1000, whose binary equivalent is 8. This means, our binary subtraction is correct.
Method of Converting the Binary to the Digital Equivalent
Now lets us see how the binary equivalent is converted to its digital form. Consider the following figure.

Binary To Decimal Conversion
The number considered is 1010. So to convert to its digital or base ten, equivalent, we need to multiply each digit with its weight. For each digit in binary equivalent, weight is assigned to get the decimal equivalent. The weights assigned are fixed for all binary representations.
So we have, 1010 when multiplied with weights as shown, we get the numerical equivalent as ten. In the same process, all the numbers shown in the first figure are converted into decimal equivalent. It may be noted that the weights assigned are decided based upon the base we have taken. In this case, since for the binary equivalent, the base is two, so we have taken the weights based on the powers of two. Eight is two to the power three, four is two to the power two, and so on.
If we need to calculate the octal equivalent, in that case, we need to take the base as 8. We will multiply with the power of eight. And similarly, in hexadecimal equivalent, we will take the base as 16.
Please refer to this link to know more about binary subtraction MCQs
Binary Subtraction with Borrow
Now let us take the second case in the truth table when zero is subtracted from one. In this, since zero is greater than one, hence the subtraction is not possible. So we require, borrow. Consider the following figure.
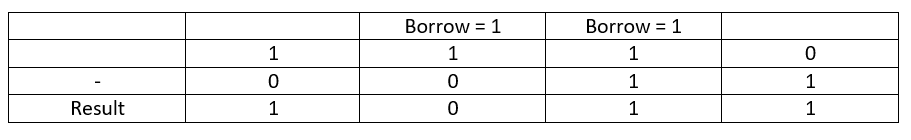
Binary Subtraction with Borrow
Step 1.
First, we need to start from the rightmost side. The numbers are zero and one. Zero cannot be subtracted from one, as zero is a lesser number. So as per the truth table, we need to take the borrow. The borrow is taken from the next number. Once the borrow is taken the number zero becomes one. However, the difference remains one only, with borrow taken, as shown in the figure.
Step 2.
For the second step, since the borrow was given, so one doesn’t remain in its place. It becomes zero. Now the subtraction to be done is zero minus one, for which we again need a borrow to be taken. Now the borrow is taken from the number left to it. Now the problem becomes zero minus one, whose difference is one with borrow taken. Hence the result is one for this step.
Step 3.
At this point, we don’t have one left. Because when borrow was taken in the previous step, the value was decremented. So it becomes zero and the problem is zero minus zero, for which the difference is zero, with no borrow.
Step 4.
For this step, the problem is one minus zero. Since one is greater than zero, we don’t need any borrow. And the difference, in this case, is 1 with no borrow.
So the final result is 1011. Now let’s check whether the subtraction is correct or not. For this, first, we need to convert the number into its decimal equivalent. The number is 1110, and its decimal equivalent is 14. Then the other number is 0011, whose decimal equivalent is 3. Therefore, the result is now, 14 minus 3 which is equal to 11. And the binary equivalent of 11 is 1011. Which is also the result obtained. Hence our subtraction is correct. This is how we perform subtraction by the borrow method.
One’s Complement Method
The one’s complement method is used to represent the signed number. For this first, we need to understand what is signed and unsigned binary numbers.
Unsigned Binary Numbers
In unsigned binary numbers, all the digits are used to represent a number. Let us say if we want to represent 13. Its binary equivalent is 1101. In this representation, all four digits are used to represent the number. The first number is also considered to calculate the decimal equivalent. And the first number is used to multiply with its weightage.
Signed Binary Numbers
In signed binary numbers, all the digits are not used for the calculation of decimal equivalent. For example, for the same number 13, if the write, 11101, the first number represents the sign. 1 indicates it’s a negative number. Hence the binary equivalent would be -13. The signed numbers along with one’s complement and two’s complement method are used for binary addition and subtraction. Let’s see the one’s complement method.
One’s Complement Method
In one’s complement method, each of the numbers of represented oppositely. Consider the following.

One’s Complement Method
The first number is two, which is in its unsigned representation. So we can say that all the numbers can be used to represent the number. Hence the binary equivalent of two is 0010. But if we consider the number -1. In this case, we have shown the signed representation. So the first digits are reserved for a sign. And since it negative number, we will complement all digits. Complement means replacing zero with ones and ones with zeros. So the number now becomes 1110.
Two Complement Method
For two’s complement method, first, we convert the number to its one’s complement form and add one to it. Consider the following.
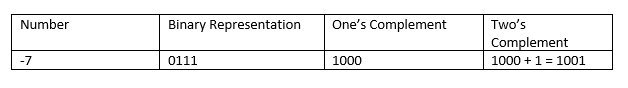
Two’s Complement
In this, the number -7 has been represented in its two’s complementary form. For that, first what we do is, convert the number into a binary representation. WE would get, 0111. Then find the one’s complement by replacing one’s with zero and zero with one. So we will get, 1000. Then add one to it, which would result in 1001, which is the two’s complement of -7.
Binary Subtraction with One’s Complement Method
For this, first, we need to convert the number into in the one’s complement, and then add the two numbers. Consider the following subtraction. Consider the following figure.
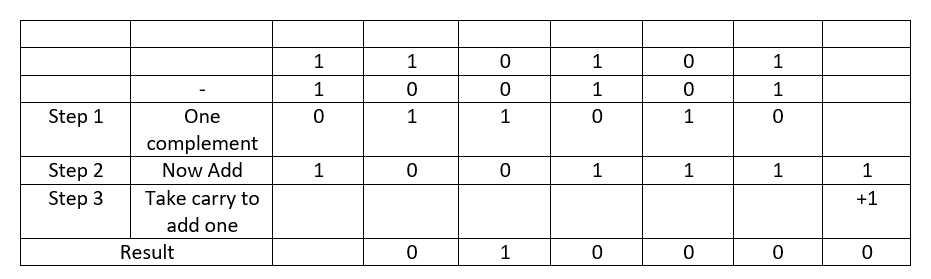
Binary Subtraction with One’s Complement
Let us say we want to subtract, 110101-100101. So first, we need to convert the second number 100101 to its one’s complement form, which is equal to 011010. Now we add the one’s complement number and the first number together, which means 110101+011010= 1001111.
Now if we have extra carry at the end, then we need to add one to the obtained result. Otherwise, this step is not necessary. So now the addition becomes 01000 which is the final result. In this manner, we do the subtraction using the one’s complement method. The same can be extended to do the binary subtraction using two’s complement method.
Binary Subtraction with Two’s Complement Method
Consider the following table. In this problem, we are subtracting 110110-010110. (Decimal equivalent 54-22)

Subtraction with Two’s Complement
Step 1. To subtract using two’s complement, first we need to find the two’s complement of the second number i.e. 010110. For this, first calculate one’s complement (which is 101001), and then add one to it. Which results in 101010
Step 2. Now we need to add the first number to the obtained two’s complement number. Which results in 110110+101010=1100000. Since it’s a six-digit representation, we need to drop the last carry. So it would be 100000
Step 3. Now the answer for the subtraction is 100000. Check with the decimal equivalent, it would be 54-22=32.
In one’s complement form, 0 is also represented to represent the sign of the number. It can have two representations, but in two’s complement form, it’s not like that. That is when we can use binary subtraction using one’s complement or two’s complement method.
3 Bit Binary Subtractor
The logic gate diagram for the three-bit subtractor is shown in the figure. As it can see that, a subtractor circuit can be easily realized using half subtractor circuits. In the three-bit subtractor circuit, the two bits are assigned for the magnitude of the number and the last number is assigned for the borrow.
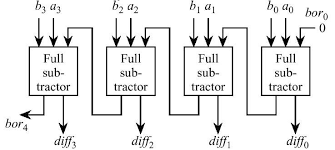
3 Bit Subtractor
As shown, the borrow is carried forward from every stage to the next stage. The circuit could be realized using logic gates. From the truth table of subtractor, the difference is equal to the output Ex-OR gate circuit and the borrow could be realized using, a compliment or not gate. Similarly, any n-bit subtractor can be easily designed and implemented. Interestingly the same circuit can be used to design n bit adder and subtractor. These are all well-known combinational logic circuits. A simple example is the multiplexer circuit.
What are subtraction integer rules?
The rules can be represented using a truth table. In simple words, when the larger number is subtracted from a smaller number, no borrow is required, else borrow is required.
What is the rule for subtracting positive and negative integer numbers?
To subtract the negative number, it is converted to its two’s complement form.
How do you subtract an integer from another integer without using a number line or counters to give an example?
We need not subtract one integer from another, without using a number line. We add them. If the signs of both are negative or positive, we simply add the numbers. But if the sign is different then we subtract.
What is the rule when subtracting integers with opposite signs?
You need not subtract integers with opposite signs, we just need to add them. In other words, it is done by adding the absolute values.
Hence, we have seen the rules for doing binary subtraction. The most common method is done by doing the two’s complement method. In real-time applications, these circuits are implemented by designing the logic circuits and implementing the same. Here is a question for you, what is binary addition?