The origins of Ladder Logic can be traced back to the world of relay-based control systems. In the early days of industrial automation, electrical engineers used relay circuits to control machinery. These circuits were represented graphically using ladder diagrams, where horizontal lines (rungs) represented power circuits, and vertical lines represented relay contacts and coils. As PLCs emerged to replace traditional relay systems, the graphical representation of ladder diagrams seamlessly transitioned into Ladder Logic programming. This visual language made it easier for engineers and electricians to understand and transition from traditional relay control to the digital realm of PLCs. In this article, we will explore the intricacies of Ladder Logic, its key features, application scenarios, and its enduring relevance in the ever-advancing landscape of industrial automation.
Graphical Representation of Ladder Logic:
Ladder Logic gets its name from the characteristic graphical representation that resembles a ladder. The programming environment displays a series of horizontal lines (rungs), and each rung represents a specific control operation or sequence. The key elements of Ladder Logic include:
Ladder Logic
Contacts (Switches):
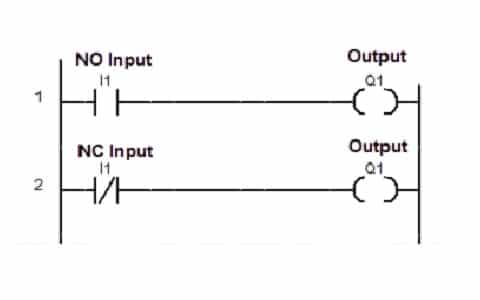
Contacts represent input conditions or switches. They can be normally open (NO) or normally closed (NC), simulating the behavior of physical switches in an electrical circuit.
Example:
−−[]−−−−[]−−, where the brackets represent a normally open contact.
Coils (Outputs):
Coils represent output actions or devices. They can be energized or de-energized based on the logical conditions in the contacts.
Example:
−−()−−−−()−− , where the parentheses represent a coil.
Power Rails:
Power rails run vertically on either side of the ladder diagram and provide electrical power to the components on the rungs.
Example: ∣∣∣∣
Rungs:
Rungs are the horizontal lines that contain a series of contacts and coils. Each rung represents a unique control sequence.
Example: −−[]−−()−−−−[]−−()−−
Key Features of Ladder Logic:
Intuitive Design:
Ladder Logic’s graphical representation is intuitive and closely mirrors traditional relay diagrams. This design makes it accessible to individuals with a background in electrical engineering.
Sequential Execution:
The execution of this Logic programs is sequential, from left to right and top to bottom. This sequential nature makes it easy to follow the flow of logic and understand the program’s behavior.
Discrete Logic Operations:
Ladder Logic excels at representing discrete logic operations such as AND, OR, and NOT. This makes it suitable for applications with discrete inputs and outputs, such as manufacturing processes and traffic control systems.
Easy Debugging:
The graphical nature of this Logic facilitates easy debugging. Engineers can visually inspect ladder diagrams to identify faults or logical errors.
Mimics Relay Logic:
Ladder Logic retains the conventions of traditional relay logic, making it a natural transition for those familiar with relay-based control systems.
Components of Ladder Logic Programs:
Input Conditions (Contacts):
Ladder Logic programs begin with input conditions, represented by contacts. These conditions are typically sensors, switches, or other inputs that initiate the control sequence.
Logic Operations:
The body of the ladder diagram contains various logic operations, including AND, OR, and NOT. These operations determine the logical relationships between input conditions.
Output Actions (Coils):
The output actions, represented by coils, define the desired outcome based on the logic conditions. These can include activating motors, opening or closing valves, or triggering alarms.
Timers and Counters:
It supports the integration of timers and counters, allowing for the creation of time-based and count-based control sequences.
Branching and Jumping:
Conditional branching and jumping instructions enable the creation of more complex control structures within the sequential execution of the program.
Applications of Ladder Logic:
Manufacturing Processes:
It is extensively used in manufacturing environments to control conveyor systems, assembly lines, and robotic processes. Its ability to represent sequential logic makes it well-suited for coordinating complex manufacturing operations.
Traffic Control Systems:
In traffic control systems, Ladder Logic can be employed to manage traffic lights and signals. The discrete nature of Ladder Logic aligns with the on/off behavior required for controlling traffic flow.
Packaging Machinery:
Packaging machines often utilize Ladder Logic to coordinate the precise movements of conveyors, sorting mechanisms, and packaging equipment. The graphical representation allows engineers to design and implement control logic with ease.
Water Treatment Plants:
It is prevalent in water treatment plants, where it is used to control pumps, valves, and filtration systems. The ability to represent discrete control operations aligns with the on/off nature of many water treatment processes.
Elevator Control Systems:
Elevator control systems leverage Ladder Logic to coordinate the operation of motors, doors, and safety features. The sequential nature of Ladder Logic is well-suited for managing the step-by-step process of elevator operation.
Programming Best Practices:
Use of Descriptive Labels:
Clearly label contacts, coils, and other elements with descriptive names to enhance program readability and understanding.
Structured Organization:
Organize the ladder diagram in a structured manner, with input conditions at the beginning and output actions at the end of each rung. This facilitates easy navigation and maintenance.
Documentation:
Provide comprehensive documentation for the Ladder Logic program, including comments and annotations. This documentation aids in troubleshooting and future modifications.
Testing and Simulation:
Prior to deploying a Ladder Logic program in a live environment, thoroughly test and simulate its behavior. Simulation allows for the identification and correction of errors without the risk of disrupting actual processes.
Example of Ladder Logic Program:
Ladder Logic program for a start-stop motor control scenario.
–[ Start Button ]—-[ Motor Coil )–[ Stop Button ]–
In this example, we’ll use two push buttons: one for starting the motor (Start button) and another for stopping the motor (Stop button). The motor will be represented by a coil.
Start Button (Normally Open Contact):
The leftmost part of the ladder diagram represents the Start button. It is a normally open contact, symbolized by “–[ ]–“. This means the contact is closed (or active) only when the Start button is pressed.
Motor Coil:
In the middle, there is the Motor Coil, represented by “–( )–“. This coil represents the motor and will be energized when the Start button is pressed.
Stop Button (Normally Closed Contact):
On the right side, there is the Stop button represented by “–[ ]–“. However, notice the orientation of the brackets; it is a normally closed contact. This means the contact is normally closed and becomes open (inactive) when the Stop button is pressed.
Execution Flow:
When the Start button is pressed, the normally open contact associated with it closes, allowing current to flow to the Motor Coil. The Motor Coil energizes, and the motor starts running.
Simultaneously, the normally closed contact associated with the Stop button opens, breaking the circuit. Even if the Stop button is pressed, it won’t affect the operation because the normally closed contact is already open.
Stop Operation:
To stop the motor, the Stop button must be pressed. This action opens the normally closed contact associated with the Stop button, breaking the circuit to the Motor Coil. The Motor Coil de-energizes, and the motor stops.
This simple Ladder Logic program demonstrates the basic principles of control in industrial automation. It uses the graphical representation to show the sequential flow of logic, making it easy to understand and troubleshoot. The start-stop motor control scenario is a fundamental example, but in real-world applications, Ladder Logic can be extended to control more complex processes and machinery by adding additional rungs and incorporating timers, counters, and other logical operations.
Future Trends and Adaptations:
As industries evolve towards greater connectivity and automation, the role of ladder Logic continues to adapt. Integration with higher-level programming languages, the incorporation of advanced communication protocols, and compatibility with Industry 4.0 principles are becoming increasingly relevant. Ladder Logic remains a foundational element, often used in conjunction with other programming languages to create comprehensive control systems that meet the demands of modern industrial processes.
Please refer to this link for Ladder Logic MCQs.
From controlling manufacturing processes to orchestrating traffic signals, Ladder Logic continues to play a pivotal role in shaping the efficiency and reliability of industrial automation.